When people say you should maximize happiness, what does that mean? Let’s say we’re measuring happiness in a unit called utils1. If you only maximize utils right now, well, you’d probably just take drugs. This doesn’t seem like a good idea; we care about our future happiness too. So maybe you think it’s not your happiness at this one moment, but it’s your happiness over time.

This additional dimension of time makes things a lot more complicated. How do we compare our happiness in the future to what we have right now? One simple way to think about this is to take the area under the curve if we plot utility against time2.

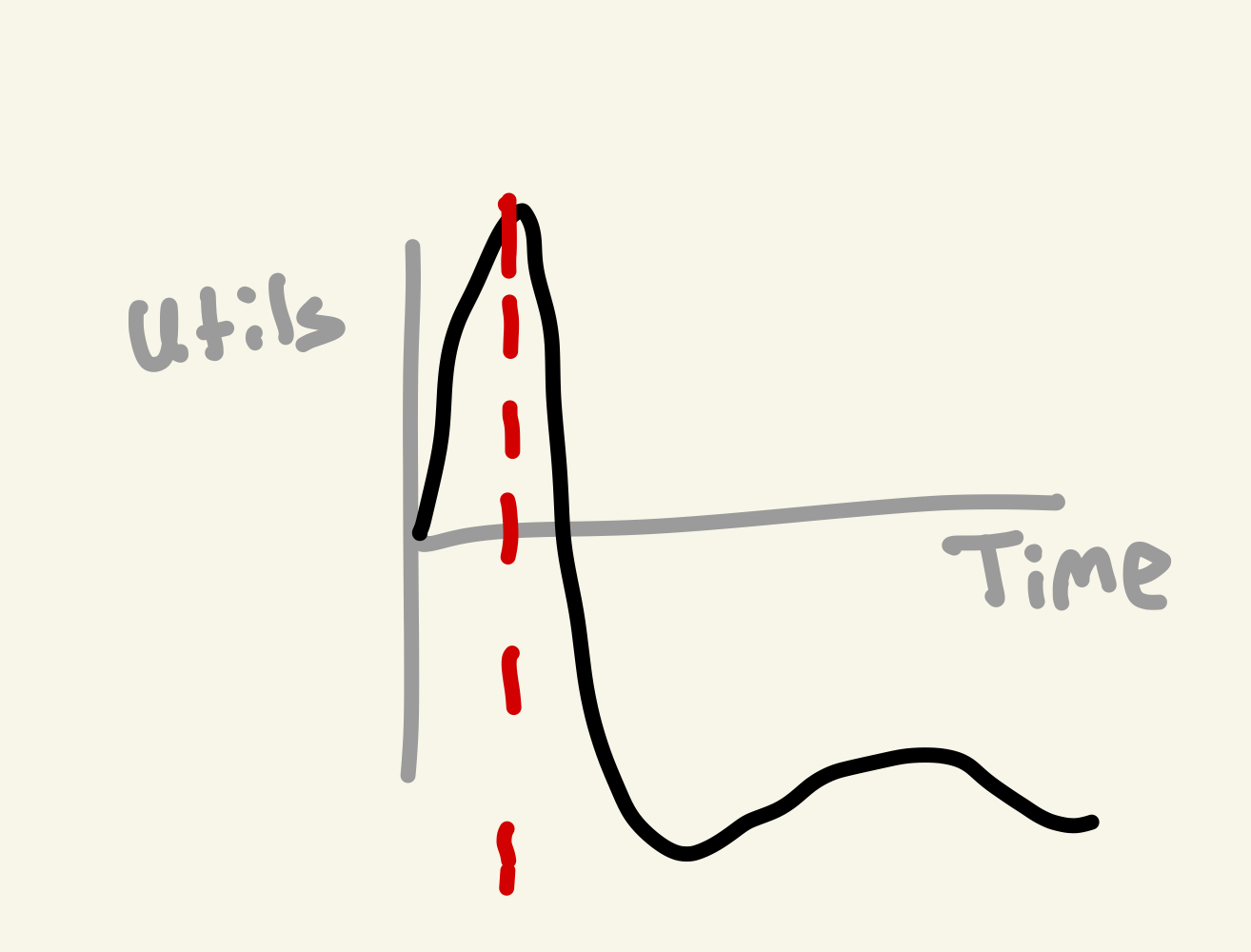Happiness curve at moment A graph of utility. At the present moment (the red dotted line), we maximize our happiness but we ignore the consequences of the future.

vs.

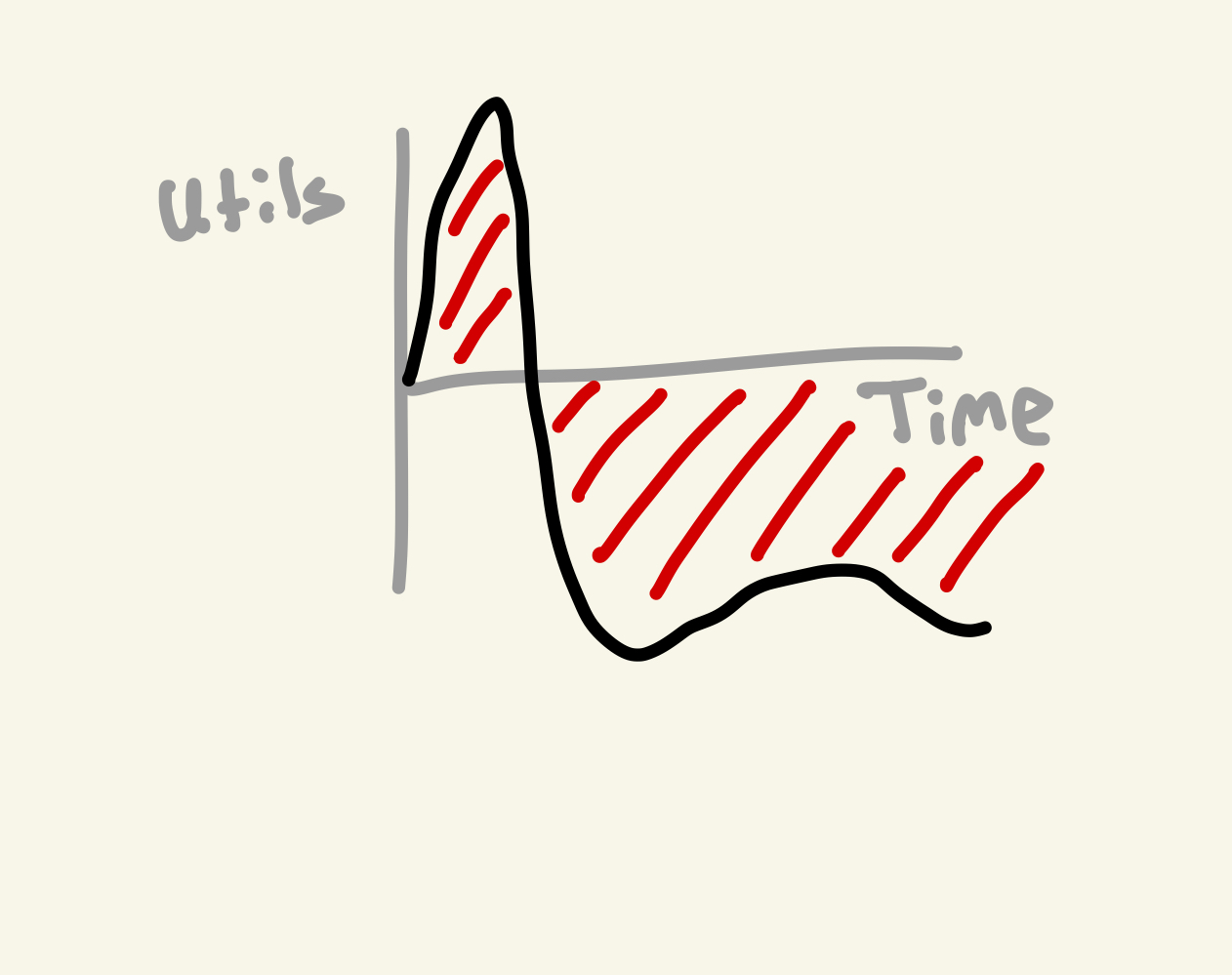Happiness curve area under curve The area under the curve — more precisely the area between the curve and the baseline axis, where it contributes negatively when below it.

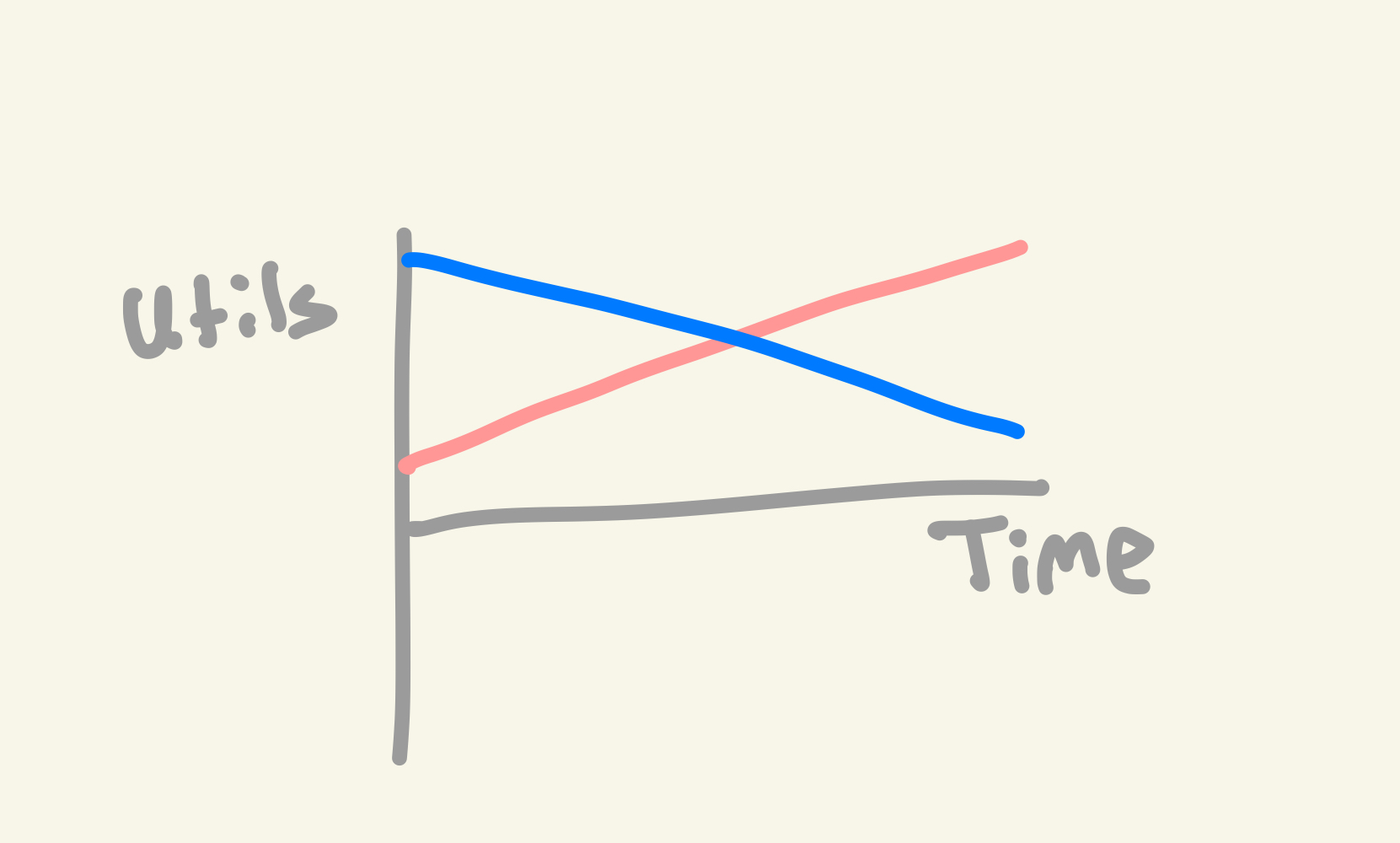
This lines up with the intuition that we care about the future. But something about this still feels wrong. Look at these two utility curves: Happiness curves with same area

Both curves cover the same area, so should we be indifferent between them? Probably not. The increasing pink line seems like a more favorable life, because we’re constantly improving. It seems that while we care about the area under the curve, what we perceive in each moment is how our utility compares to what it was before and that has an effect on our original utility.

Maybe what we value here at any moment $x$ is roughly $f(x) - f(x - \epsilon)$ for some $\epsilon$ look-back period. One way I visualize this is that the axes themselves move at a delayed rate relative to where you currently are.

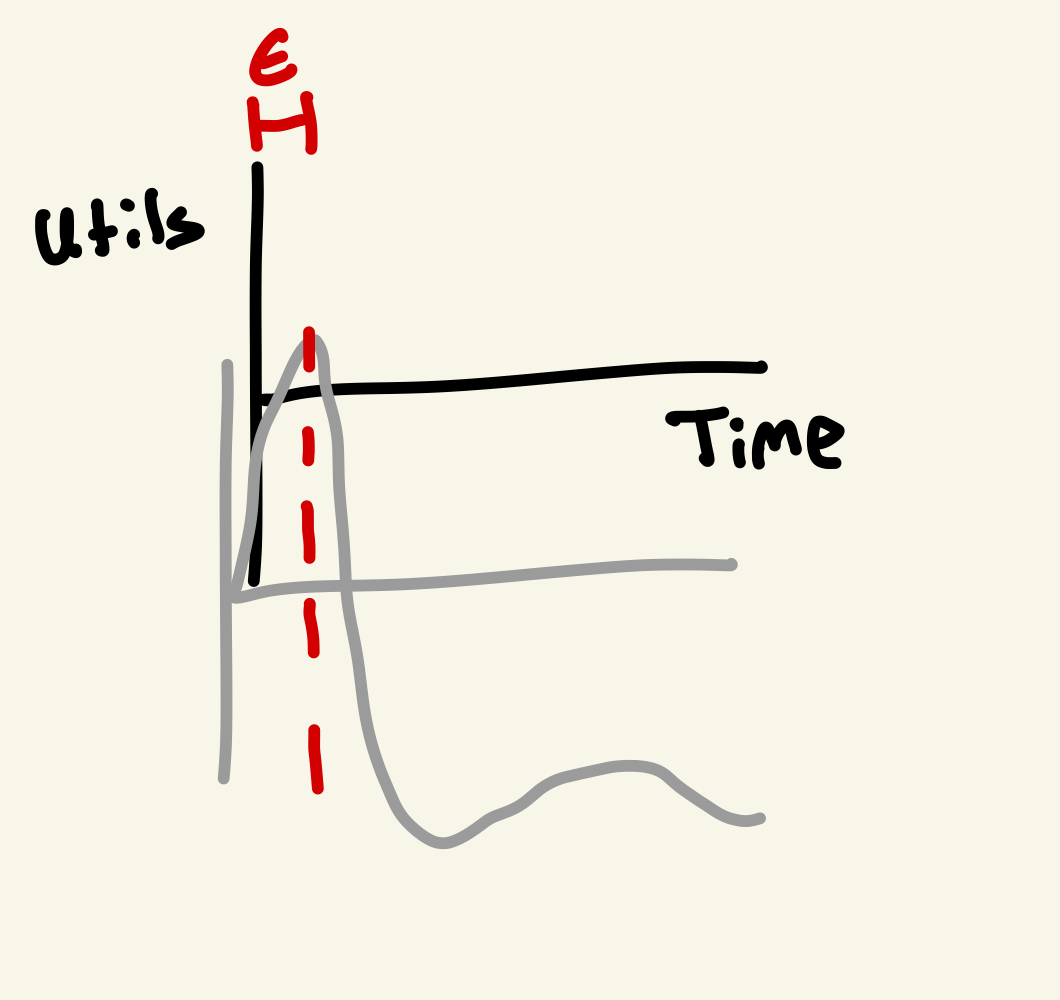Happiness curves with shifting baseline If $\epsilon$ was 1 day, this is saying every day, you perceive your happiness relative to how you felt the day before

So at any moment in time, you move your axes to be centered around where you were at $x-\epsilon$ and evaluate your position then. This is roughly the same as considering $f’(x)$.

Now some people might point out that a true utility curve already bakes this information in, which is valid. I make this distinction: the original utility curve is what it would be if you never thought about your happiness and just went along life. My argument here is that the perception of your utility curve affects your utility itself. This means we really should be considering $f(x) + \alpha \cdot f’(x)$ for some factor $\alpha \geq 0$.

You can go down this rabbit hole again and say that you care about the acceleration at which your happiness is improving, roughly $f^″(x)$, which means your real utility is $f(x) + \alpha \cdot f’(x) + \beta \cdot f^″(x)$ with $0 \leq \beta$ and probably $\beta « \alpha$. You can keep extending this, but people probably don’t think beyond the second derivative of their happiness (I certainly don’t).

I feel for most people (at least me), $\alpha$ is pretty large ($\beta$ is pretty negligible). We often compare happiness to the past—talking about “the good old days” or reminiscing about the past. Being present and exercising gratitude lowers $\alpha$ by realizing that all that really matters is how we feel in the moment3.

I think, though, it’s pretty hard to get $\alpha$ low. It’s already hard enough to avoid comparing yourself to others (and often, the advice given is “compare yourself to where you were before, not to others”). So given $f’(x)$ is a non-negligible term, how do we optimize happiness?

Integrating the new happiness model gives $(\int_0^1 f(x) dx)+ \alpha \cdot (f(1) - f(0))$, assuming your life is lived on $x \in [0, 1]$. This is the same as the area under the curve plus an additional term for how much we’ve changed in absolute utility. What this is to say is that the overall growth of your happiness matters here, according to some $\alpha$.

Now this might be a duh result, but I feel like writing this out helps justify some of my beliefs. One thing I believe is that the correlation between wealth and happiness isn’t that large, after some point4. Even if billionaires have more absolute utils than I do due to their wealth, if $\alpha$ is high, they might not be that much happier because of the perception that their happiness is stagnating. Thinking back to the moving axes example, no matter how much “absolute” utility they gain, the baseline is always resetting. I think this also holds true for the reverse direction—it reconciles how people with significantly less money still have lives that feel just as happy as others.

This also explains why lifestyle inflation isn’t super great; you’re optimizing for the short-term, but the baseline is going to keep resetting.

That said, I think there’s too much of an emphasis on optimization, so I definitely don’t/wouldn’t think about every action I do through this lens. But I think it gives interesting heuristics on how to view your life. Maybe you also come to different results if you take different assumptions. For example, there’s no fundamental reason to prefer the area under the curve; perhaps you care about maximizing the minimum happiness.

Maybe this post is also just a way to combine my love for math and philosophy 😁

  1. Some might argue that happiness can’t be measured, but I think there’s legitimate ways like the number of dopamine molecules released in your body. Obviously no one is calculating this, but it must be true that utility can be somewhat be measured and compared. ↩

  2. Measuring the area under the curve might make you uneasy because there’s a lot of uncertainty as time passes on how many utils you might have in the future at any given moment. Let’s just take it from a birds-eye view as if we’re objectively trying to quantify the utility from someone’s life. ↩

  3. $\alpha$ being high isn’t always bad though! If $f’(x)$ is large, maybe having a high $\alpha$ is great. ↩

  4. Obviously having money solves problems and is useful. ↩